Exp Fluids  DOI 10.1007/s00348-009-0779-2

Approach to local axisymmetry in a turbulent cylinder wake
Jianchun Mi  R. A. Antonia

The objective of this experimental study is to characterise the small-scale turbulence in the intermediate wake of a circular cylinder using measured mean-squared velocity gradients. Seven of the twelve terms which feature in e, the mean dissipation rate of the turbulent kinetic energy, were measured throughout the intermediate wake at a Reynolds number of Red = 3000 based on the cylinder diameter (d). Earlier measurements of the nine major terms of e by Browne et al. (J Fluid Mech 179: 307–326 1987) at a downstream distance (x) of x = 420d and Red = 1170 are also used. Whilst departures from local isotropy are significant at all locations in the wake, local axisymmetry of the small-scale turbulence with respect to the mean flow direction is first satisfied approximately at x = 40d. The approach towards local axisymmetry is discussed in some detail in the context of the relative values of the meansquared
velocity gradients. The data also indicate that axisymmetry is approximately satisfied by the large scales at x/d C 40, suggesting that the characteristics of the small
scales reflect to a major extent those of the large scales. Nevertheless, the far-wake data of Browne et al. (1987)show a discernible departure from axisymmetry for both
small and large scales.

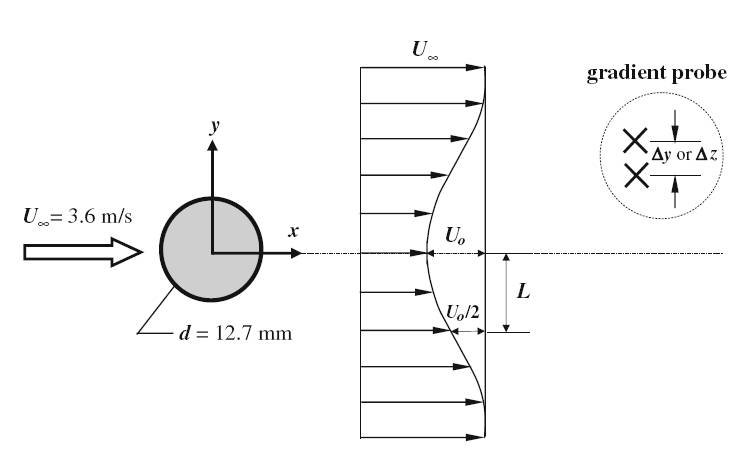
Fig.1 Sketch of experimental arrangement, coordinate system and gradient measurement probe, with notations

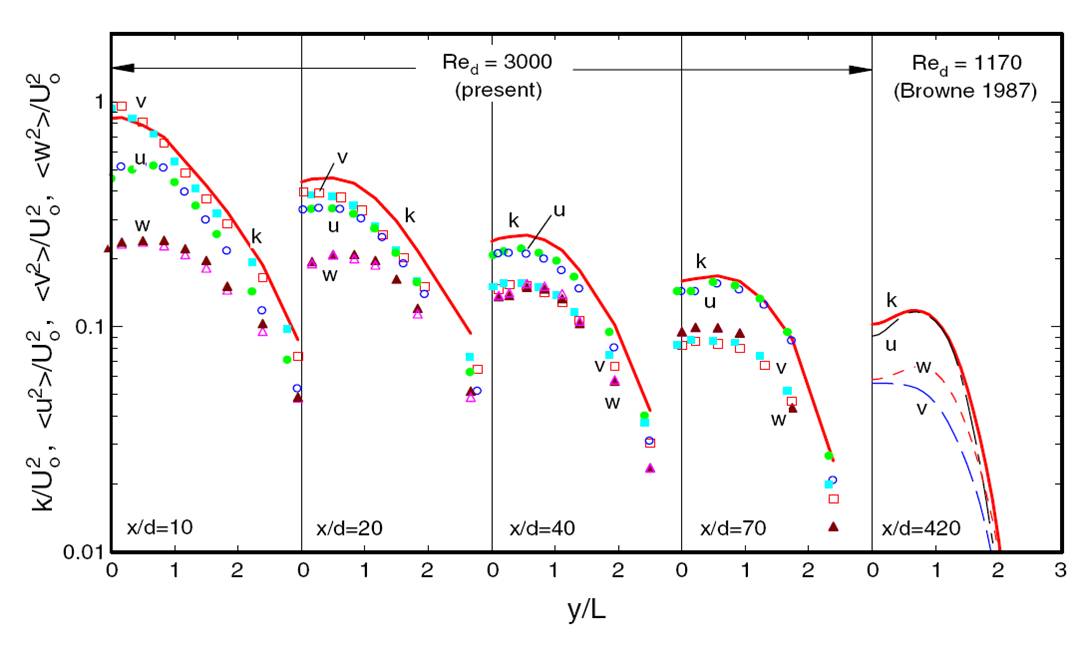
Fig.2 Lateral normalised profiles of the turbulence kinetic energy k and Reynolds normal
stresses at different x locations as indicated on the plots. Present data are for x/d = 10–70, and Browne et al.’s (1987) data are at x/d = 420

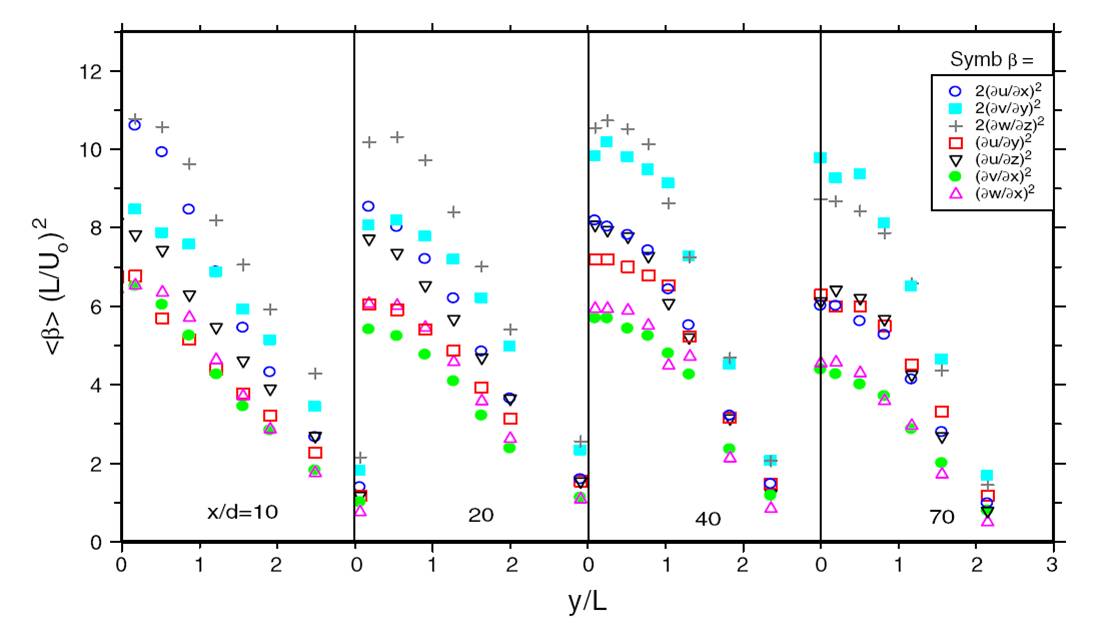
Fig.3 Lateral profiles of the normalised gradients of velocity fluctuations at different x/d
locations, as indicated on the plot

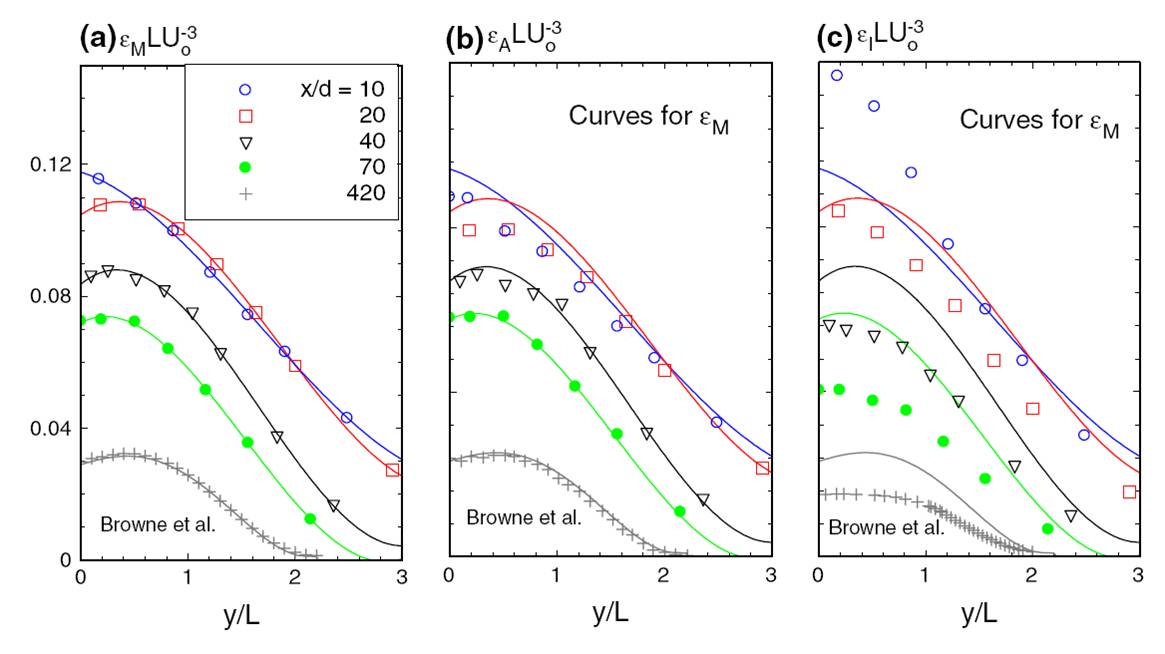
Fig.4 Lateral profiles of the dissipation rates estimated in different ways. a  estimated
using (3) and local axisymmetry for the unmeasured last five terms; b estimated only
using (18) for local axisymmetry; c estimated only using (9) for local isotropy. Fits in part a are also shown in parts b and c for comparison

For detailes: http://www.springerlink.com/content/r818870g68l5w1l6/